Pendahuluan

Halo Jawara POSI! Permutasi dan kombinasi adalah dua konsep kunci dalam matematika yang digunakan untuk menghitung kemungkinan pengaturan dan pemilihan dari suatu set objek. Meskipun kedua istilah ini sering digunakan bersamaan dan terdengar serupa, mereka memiliki aplikasi dan formula yang berbeda.

Artikel ini akan menjelaskan perbedaan antara permutasi dan kombinasi, memberikan contoh yang relevan, dan menunjukkan bagaimana mereka dapat diaplikasikan dalam berbagai situasi praktis.

Apa Itu Permutasi?

Permutasi adalah pengaturan semua atau sebagian dari sejumlah objek dengan mempertimbangkan urutan. Dalam permutasi, urutan penempatan objek sangat penting. Sebagai contoh, katakanlah Anda memiliki tiga buku A, B, dan C. Jika Anda ingin tahu berapa banyak cara buku-buku tersebut dapat diatur di rak, Anda menggunakan permutasi karena urutan buku akan mempengaruhi pengaturannya.

Rumus dasar untuk permutasi adalah

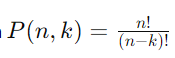
dimana:

• 𝑛 adalah jumlah total objek.
• 𝑘 adalah jumlah objek yang akan diatur.
• 𝑛! menunjukkan faktorial dari 𝑛n, yaitu hasil kali semua bilangan bulat positif hingga 𝑛n.

Mengenal Kombinasi

Berbeda dengan permutasi, kombinasi berfokus pada pemilihan objek tanpa mempertimbangkan urutan. Ini digunakan ketika kita ingin mengetahui berapa banyak cara untuk memilih sejumlah objek dari grup yang lebih besar, di mana urutan tidak relevan. Misalnya, jika Anda memiliki 5 bunga dan ingin membuat buket dengan 3 bunga, Anda akan menggunakan kombinasi untuk menentukan berapa banyak pilihan buket yang mungkin.

Rumus untuk kombinasi adalah

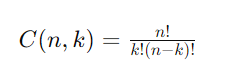
di mana:

• 𝑛 adalah jumlah total objek yang tersedia.
• 𝑘 adalah jumlah objek yang dipilih.

Perbandingan dan Contoh Penggunaan

Untuk memahami lebih lanjut, mari kita bandingkan penggunaan permutasi dan kombinasi melalui contoh sederhana:

• Permutasi: Anda memiliki 3 hadiah yang akan diberikan kepada 3 orang. Berapa banyak cara berbeda yang bisa Anda berikan hadiah-hadiah tersebut, dengan mempertimbangkan bahwa setiap orang mendapatkan satu hadiah? Ini adalah kasus permutasi karena urutan pemberian hadiah mempengaruhi hasilnya.
• Kombinasi: Anda ingin memilih 3 kandidat dari grup 10 orang untuk sebuah komite. Berapa banyak cara untuk memilih kandidat? Ini adalah kasus kombinasi karena urutan seleksi tidak penting.

Aplikasi Praktis Permutasi dan Kombinasi

Permutasi dan kombinasi digunakan luas dalam berbagai bidang seperti statistik, riset operasi, teori peluang, dan bahkan dalam kehidupan sehari-hari. Beberapa aplikasi umum meliputi:

• Pengkodean dan Keamanan Cyber: Menggunakan permutasi untuk membuat kata sandi yang rumit.
• Penelitian Klinis: Menggunakan kombinasi untuk menentukan berbagai kelompok pasien untuk pengujian obat.
• Pengorganisasian Acara: Menyusun jadwal atau daftar tamu dengan permutasi.

Contoh Soal Permutasi dan Kombinasi

Untuk memberikan pemahaman yang lebih konkret mengenai permutasi dan kombinasi, berikut adalah beberapa contoh soal yang dilengkapi dengan penyelesaian:

Soal Permutasi: Mengatur Buku

Anda memiliki empat buku yang berbeda: Matematika, Fisika, Kimia, dan Biologi. Berapa banyak cara yang mungkin untuk mengatur keempat buku tersebut pada sebuah rak?

Penyelesaian: Jumlah total cara untuk mengatur keempat buku tersebut adalah faktorial dari 4 (jumlah buku), yang dinyatakan sebagai 4!

4! = 4 x 3 x 2 x 1 = 24

Jadi, ada 24 cara yang mungkin untuk mengatur keempat buku tersebut.

Soal Kombinasi: Memilih Anggota Tim

Dalam sebuah kelas terdapat 15 siswa. Guru tersebut ingin membentuk sebuah tim debat yang terdiri dari 3 siswa. Berapa banyak kombinasi yang mungkin dalam memilih 3 siswa dari 15 siswa tersebut untuk membentuk tim debat?

Penyelesaian: Untuk menyelesaikan ini, kita gunakan rumus kombinasi 𝐶(𝑛,𝑘), dimana 𝑛n adalah jumlah total siswa dan 𝑘k adalah jumlah siswa yang dipilih.

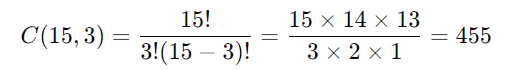
Kesimpulan

Memahami permutasi dan kombinasi dapat secara signifikan memperkuat keterampilan pemecahan masalah dan kemampuan analitis. Konsep-konsep ini tidak hanya penting dalam matematika tetapi juga dalam pengambilan keputusan sehari-hari dan pengembangan strategis di banyak bidang profesional.

Topik ini dapat kamu temukan di buku Jenius Olimpiade Sains (JOS) yang ada di POSI Store! Dapatkan segera di marketplace kesayangan kamu atau hubungi Admin POSI Store di sini

Follow POSI di Instagram, Twitter, Tiktok, dan jangan lupa subscribe di Youtube POSI.

Dapatkan informasi lebih lengkap seputar produk dan layanan POSI subscribe ke POSI.id dengan cara mengisi pop-up yang muncul di laman website.

Cek informasi dan artikel menarik di Blog POSI.

Pertanyaan, keluhan, dan saran seputar produk dan pelayanan POSI, kirimkan email ke [email protected] dan telepon ke call center POSI di (+62) 821 6544 1992.

Informasi seputar kompetisi online dan offline POSI di 2024, kamu bisa cek di Instagram @posikompetisi atau cek di sini!