Halo Jawara POSI! Persamaan Diophantine adalah jenis persamaan matematika yang solusinya hanya diperbolehkan dalam bilangan bulat. Konsep ini dinamakan dari matematikawan Yunani kuno, Diophantus dari Alexandria, yang karyanya dianggap sebagai salah satu sumber terawal dalam penanganan persamaan ini.
Artikel ini akan menggali lebih dalam tentang definisi persamaan Diophantine, contoh soal, serta aplikasinya dalam matematika modern.
Contents
Apa Itu Persamaan Diophantine?
Persamaan Diophantine melibatkan dua atau lebih variabel dengan koefisien bilangan bulat dan hanya mencari solusi di mana semua variabel adalah bilangan bulat. Biasanya digunakan dalam teori bilangan tetapi juga memiliki aplikasi dalam bidang lain seperti kriptografi dan algoritma komputasi. Persamaan ini menarik karena tidak selalu memiliki solusi, dan jika ada, bisa lebih dari satu atau bahkan tak terbatas.
Contoh sederhana dari persamaan Diophantine adalah persamaan 2𝑥+3𝑦=52x+3y=5. Persamaan ini meminta kita untuk mencari semua pasangan bilangan bulat 𝑥 dan 𝑦 yang menjadikan persamaan tersebut bernilai benar.
Contoh Soal
Untuk memberikan gambaran yang lebih jelas, mari kita lihat contoh soal:
Soal: Temukan semua pasangan bilangan bulat (𝑥,𝑦) yang memenuhi persamaan Diophantine 7𝑥+5𝑦=127x+5y=12.
Pendekatan Penyelesaian: Langkah pertama dalam menyelesaikan persamaan ini adalah dengan mencari solusi khusus. Kita dapat memulai dengan mencoba beberapa nilai bilangan bulat untuk 𝑥 dan 𝑦 dan melihat apakah mereka memenuhi persamaan.
Setelah menemukan satu set solusi, langkah berikutnya adalah mengeksplorasi apakah ada solusi lain. Dalam kasus persamaan linear seperti ini, solusi tambahan dapat ditemukan dengan menggunakan kombinasi linier dari solusi khusus.
Solusi: Misalnya, kita mulai dengan 𝑥=1x=1 dan coba cari 𝑦 yang memenuhi. Substitusi ke dalam persamaan memberikan:
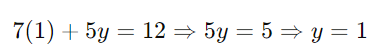
Jadi, satu solusi adalah (𝑥,𝑦)=(1,1). Untuk mencari solusi lain, kita bisa menggunakan metode pergeseran berdasarkan kelipatan terkecil dari koefisien variabel
lain, tetapi untuk kasus ini, hanya akan ada satu solusi yang memenuhi kondisi bilangan bulat.
Signifikansi dan Aplikasi
Persamaan Diophantine tidak hanya sebuah tantangan teoretis dalam matematika tetapi juga memiliki aplikasi praktis yang signifikan. Salah satu aplikasi modern adalah dalam kriptografi, di mana persamaan semacam ini digunakan untuk mengamankan transaksi digital. Selain itu, dalam teori bilangan, persamaan ini membantu dalam pemecahan masalah yang berkaitan dengan bilangan prima dan komposisi bilangan.
Dalam bidang ilmiah dan rekayasa, model yang menggunakan persamaan jenis ini sering kali digunakan untuk merancang sistem yang optimal berdasarkan parameter tertentu yang hanya dapat diwakili dalam bilangan bulat. Contohnya termasuk alokasi sumber daya atau jadwal operasional yang harus mematuhi kriteria ketat.
Menghadapi Tantangan Persamaan Diophantine
Meskipun persamaan Diophantine bisa sangat kompleks dan sulit untuk diselesaikan, ada beberapa metode yang telah dikembangkan matematikawan untuk menangani kasus-kasus tertentu. Misalnya, teorema dasar aritmatika dan teknik aljabar modern sering digunakan untuk mendekomposisi dan menyelesaikan persamaan ini dalam bentuk yang lebih sederhana.
Kesulitan utama dalam menyelesaikan persamaan ini adalah tidak adanya formula umum yang dapat diaplikasikan pada semua jenis persamaan ini, yang membuat setiap masalah harus dianalisis dan diselesaikan secara individu.
Kesimpulan
Persamaan Diophantine adalah contoh menarik dari bagaimana teori matematika kuno masih relevan dan berguna dalam berbagai aplikasi modern. Meski menantang, solusi dari persamaan ini memberikan wawasan mendalam tentang struktur dan sifat bilangan.
Baik digunakan untuk aplikasi praktis atau sebagai alat dalam teori bilangan, persamaan ini terus menarik minat dan tantangan bagi matematikawan di seluruh dunia.
Dengan memahami dasar-dasar dan teknik untuk menangani persamaan Diophantine, kamu dapat lebih mendalami dan mungkin bahkan menemukan solusi untuk masalah kompleks dalam matematika dan disiplin ilmu lainnya.
Topik ini dapat kamu temukan di buku Jenius Olimpiade Sains (JOS) yang ada di POSI Store! Dapatkan segera di marketplace kesayangan kamu atau hubungi Admin POSI Store di sini
Follow POSI di Instagram, Twitter, Tiktok, dan jangan lupa subscribe di Youtube POSI.
Dapatkan informasi lebih lengkap seputar produk dan layanan POSI subscribe ke POSI.id dengan cara mengisi pop-up yang muncul di laman website.
Cek informasi dan artikel menarik di Blog POSI.
Pertanyaan, keluhan, dan saran seputar produk dan pelayanan POSI, kirimkan email ke [email protected] dan telepon ke call center POSI di (+62) 821 6544 1992.
Informasi seputar kompetisi online dan offline POSI di 2024, kamu bisa cek di Instagram @posikompetisi atau cek di sini!
